Time dilation due to different inertial frames of motion

Effect of speed on time and special theory of relativity 

According to Albert Einstein’s special theory of relativity, the time interval between two respective events is different if measured from different inertial frames. For Example, if an observer moving with some velocity sees two consecutive events in a stationary platform and if he measures the time interval between the events then he will find that the time interval observed by him is larger than the time interval observed by an observer stationary with respect to the platform.

Let’s illustrate this phenomenon with a hypothetical experiment to understand it better.

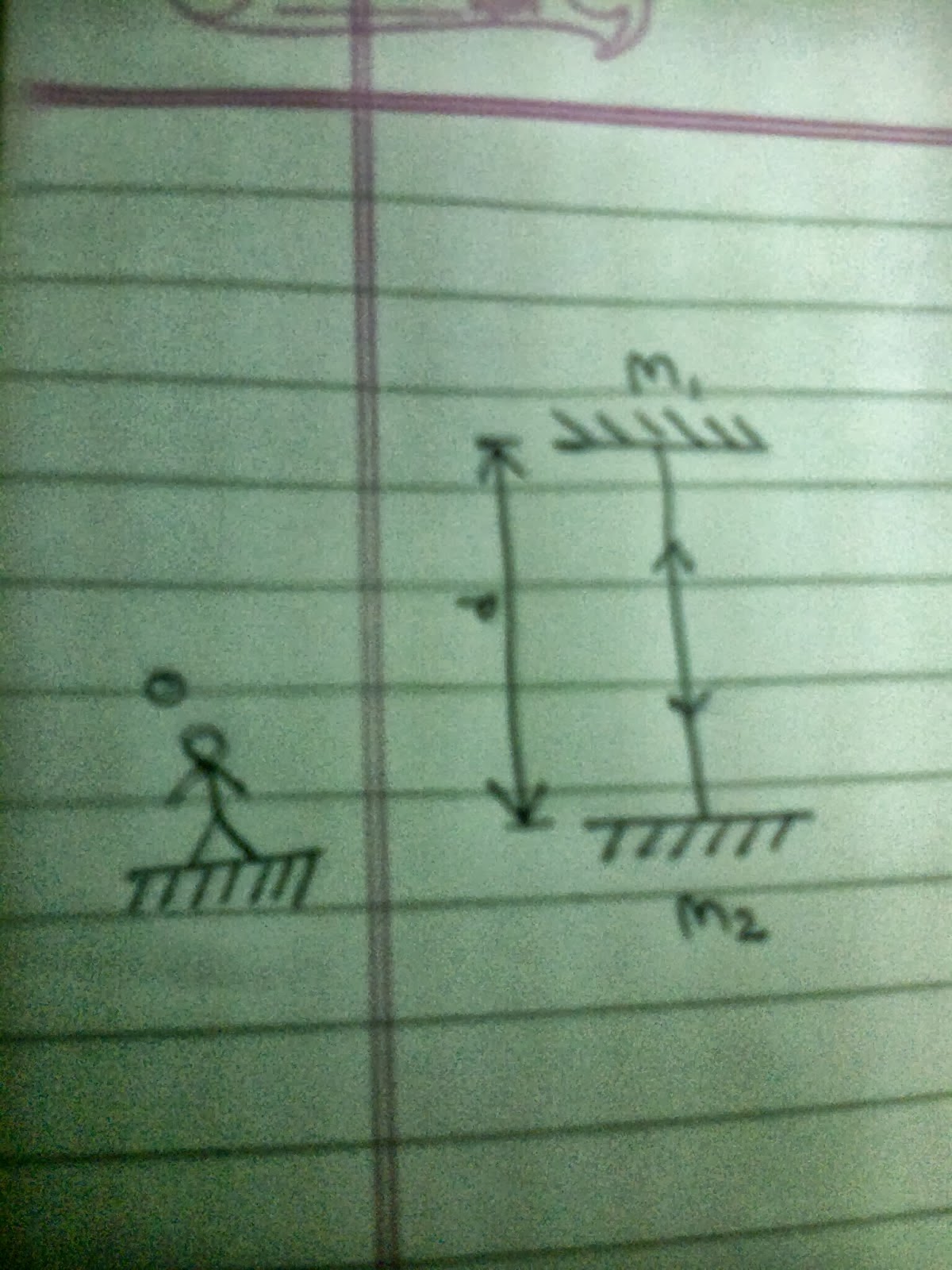
Consider that two mirrors are fixed horizontally, facing each other. Let the distance between the mirrors be‘d’, name the top mirror as M1 and lower mirror be M2. Consider an observer ‘o’ standing at a distance as shown in Fig 1.

If a light pulse is reflected back and forth by the mirrors. Let the first reflection at M1 be ‘event 1’ and the second reflection be ‘event2’.

Now we’ll find the time interval between the successive reflections from M1 and M2.

Fig 1

In the given situation, the distance traveled by light pulse between the successive reflections from M2 = 2*d

As the speed of light is 3*10 ⁸m/s, we represent it as ‘c’.

Since velocity = distance/time

Therefore c = 2d/t

Or              t = 2d/c.                                                                                        …….. eqn. 1

Now if we consider the observer to be moving, let the observer be ‘o’’.

In this frame the observer o’ is moving at a velocity of v towards observer o. according to o’ mirrors are moving towards the right with a velocity v,

                                                                           Fig 2

And mirror M2 has changed its position at the time of second reflection. If the time interval between the reflections is t’ then distance traveled by light pulse can be easily calculated by Pythagoras formulae and it comes to be

 c*t’ =  2*√ [ d ² + (v*t’/2) ² ]

Or,        (c*t’/2) ² = d ² + (vt’/2) ²

Or,        (c ² – v ²) * (t’/2) ² = d ²

Or,        t’ = 2d/√ (c ² – v ²)

Or,        t’ = (2d/c)/√ [1 – (v/c) ²]

Or,        t’ = t/√ [1 – (v/c) ²]                                                                          ………….from eqn. 1

Here, ‘v’ is always smaller than ‘c’, therefore ‘1/√ [1 – (v/c) ²]’ is always greater than 1. It shows that time measured by moving observer is more than the time measured by stationary observer for the same event. This phenomenon is called Time Dilation.
Related Articles: Space-time